Edwin Beggs - personal home page
My research is somewhere in the region of Algebra, Computer Science,
Geometry and Theoretical Physics. One connecting interest is
mathematical physics, but my approach to the subject is more related
to pure mathematics. I am a generalist rather than a specialist, and
frequently end up learning things as I go along.

A Taiko drum - I am not much good on these, usually I play Djembes.
Edwin's
publications - Google Scholar
Edwin's
official Swansea University page
Wales
Mathematical Physics - Physical Mathematics Zoom Seminar
This year I am teaching the modules for Mathematics
MA-111
- Foundations of Algebra
MA-212
- Groups and Rings
and supervising projects for the Computer Science MSc, including
Quantum Computation.
I have been involved in outreach events such as the Urdd eisteddfod
(Builth Wells) June 2018 and in June 2020 I made the 40 minute
lecture `The geometry of curved spaces' for the program `Bridging
Mathematics live lectures for Year 13 students' for the Further
Maths Support Program Wales (which, given the circumstances, was
actually a recorded lecture).
I am currently Academic Integrity representative and Ethics
representative for the Maths Dept, sit on the College of Science
Corporate Responsibility committee, and am a fire warden and first
aider in the Computational Foundry.
I was awarded a Diploma in Computing (Open University) in December
2001 and Fellowship of the HEA in 2020.
As a student I worked for three summers with Prof. Sir
William Hawthorne at the Whittle Laboratory in
Cambridge on computer simulations of fluid flow in
turbomachinery. The first summer I was employed by Cummins, and the
last two by Rolls Royce aeroengines.
Journal of Physics A: Mathematical and Theoretical
An editor of a special issue on Noncommutative Geometry and
Physics - this will be looking for papers shortly. Note that
serious Physics content will be required, not just Mathematics.

Edwin Beggs & Shahn
Majid (Queen Mary London)
Quantum
Riemannian Geometry - published March 2020.
Supercomputing Wales: A
New Decade of Supercomputing - Wales
Millennium Centre, Cardiff,
Member of expert panel discussion on Quantum Computing.
Friday 24th January 2020, 1 to 2:30
Noncommutative
geometry
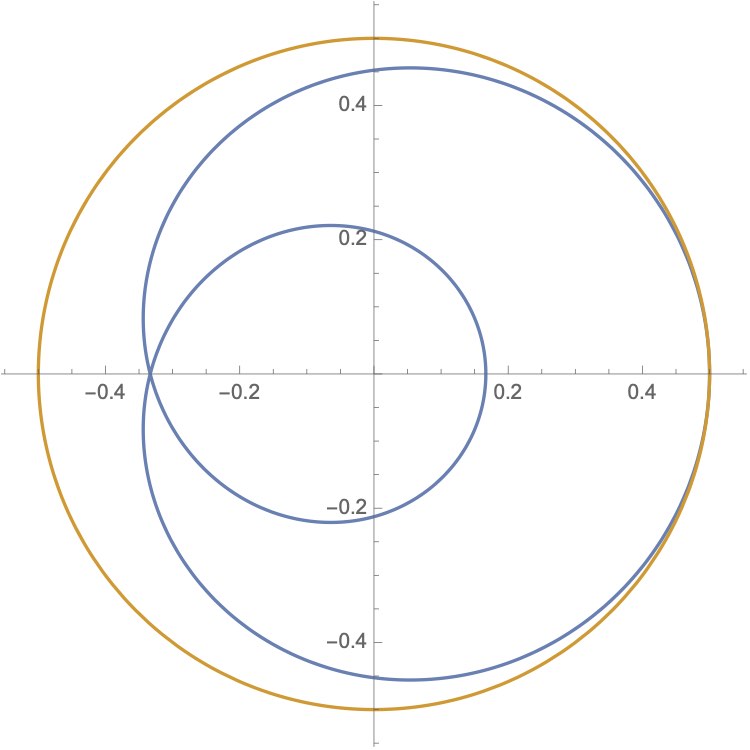
The state space of the algebra of 2 by 2 complex matrices forms a
ball in 3D real space, and the pure states are the boundary, which
is a 2-sphere. This is a picture of a 2D real plane intersecting the
state space, with the yellow circle marking the pure states. The
blue curve is the path of a geodesic in state space, for a given
calculus, connection and initial vector field on the algebra.
There are many ways to extend the ideas of classical
differential geometry to a noncommutative world. Our view is
that there is no clear answer as to which of these is correct,
given that many of them have their own rich pure mathematical
theory. However, if we were to think about what should ideally
be noncommutative differential geometry, we might identify the
following considerations. There should be a broad collection of
examples of interest across different branches of mathematics.
Noncommutative geometry should reduce to classical geometry as a
special case, though some aspects of the theory may become
trivial in the classical case. Most constructions in classical
differential geometry should have noncommutative geometry
analogues. Last but not least, as geometry originated as a
practical subject, there should be applications, which
historically has meant applications in physics and applied
mathematics.
The beginning of the preface of the book (see above).
I shall not go much into research done before the
writing of the book unless I consider it a current research
interest, the reader may look there for details. After the
publication of the book I turned to the dynamics of noncommutative
systems. Classically this often reduces to the time variation of a
point on a set, so the first place to look in the noncommutative
world is for time evolution of a state of an algebra A. For a C*
algebra the states are given by Hilbert C*-modules for the algebra
A, and by the KSGNS construction a path of states is given by a
C(R)-A Hilbert C*-bimodule. Given a calculus on the algebra and a
connection on the algebra and bimodule, it turns out that the usual
theory of bimodule connections (see book) gives the velocity of the
path and a simple form of the geodesic velocity equation,
generalising the classical differential equation for the velocity of
a geodesic. It is then quite simple to give examples of geodesics on
algebras like matrices or the Hopf algebra of functions on a group.
Edwin Beggs, Noncommutative
geodesics and the KSGNS construction, Journal of Geometry and
Physics Volume 158, December 2020, 103851
Of course this raised more problems and questions.
There was a definition of the reality of a vector field relative to
a state (yes, noncommutative vector fields exist and are not just
derivations) which was required to maintain normalisation of a time
varying state. These noncommutative vector fields had divergences,
again relative to a state. The definition of geodesic (or rather we
shall be strict and say autoparallel path) was given in terms of a
connection. Now in classical Riemannian geometry we simply plug in
the Levi Civita connection and everything is fine. In noncommutative
geometry for a given Riemannian metric there may or may not be a
Levi Civita connection. However the most annoying aspect is that
classically there is a variational derivation for the geodesic
equation, and this is a problem on the noncommutative side. It is
not that variational approaches do not work in noncommutative
geometry, e.g. there is a very nice variational approach to the
Laplacian in many cases. The variational approach to the
noncommutative geodesic equation fails because some terms pile up on
the boundary of the integral of the velocity squared terms, and
there is no obvious way to get them to behave - in other
words, there may be a nice trick to make the whole thing work. There
is also the question of whether there is a natural metric on the
state space, after the manner of Marc Rieffel's paper Compact Quantum Metric
Spaces, for which the geodesic motion has nice properties like
a uniform Lipschitz constant.
There was an obvious direction to take the
noncommutative geodesic work in. In General Relativity test
particles move along geodesics. Therefore (insert massive
disclaimers and whatever here) quantum particles ought to move along
`quantum' geodesics. The first try at this hugely over-ambitious and
likely wrong guess was asking whether in quantum mechanics (not
field theory) we could make sense of time evolution as geodesic
motion. And here, at least, the answer is yes, and is given in the
following paper by Shahn Majid and myself. Interestingly, and in
accord with several other quantum systems, we effectively have to
take a central extension of the original algebra (or in our case,
its calculus) to get things to work.
<<We show that the standard Heisenberg algebra of
quantum mechanics admits a noncommutative differential calculus
depending on the Hamiltonian and a flat quantum connection with
torsion on it such that a quantum formulation of autoparallel curves
(or `geodesics') reduces to Schrodinger's equation. The connection
is compatible with a natural quantum symplectic structure and
associated generalised quantum metric. A remnant of our approach
also works on any symplectic manifold where, by extending the
calculus, we can encode any hamiltonian flow as `geodesics' for a
certain connection with torsion which is moreover compatible with an
extended symplectic structure. Thus we formulate ordinary quantum
mechanics in a way that more resembles gravity rather than the more
well-studied idea of formulating geometry in a more quantum manner.
We then apply the same approach to the Klein Gordon equation on
Minkowski space with a background electromagnetic field, formulating
quantum `geodesics' on the relevant relativistic Heisenberg algebra.
Examples include a proper time relativistic free particle wave
packet and a hydrogen-like atom. >>
Edwin Beggs & Shahn Majid, Quantum geodesics in
quantum mechanics, arXiv:1912.13376
[math-ph]
In classical differential geometry much work goes into
the definition of the Riemann curvature tensor, and then defining
the Ricci tensor is just a contraction of indices. In noncommutative
geometry there is also a Riemann curvature tensor, but we have a
problem with Ricci. There are good cases where Ricci can be defined
(see the book and Shahn
Majid's web page) but there is no sensible general definition.
It may be related to divergences of noncommutative vector fields and
variational methods. The importance of Ricci is that it enters in
Einstein's field equations for General Relativity. It might be
thought that a noncommutative version of General Relativity would
only be relevant near the Planck length or in other extreme
circumstances, but this is not necessarily the case. Any quantum
system which has a measurable gravitational effect in principle
quantises gravity, and if that gravitational field can be made
dependent on entangled states then we may have interesting quantum
gravitational effects. Current experiments are heading in a
direction where performing such gravitational measurements are not
so unthinkable as it once was (e.g.
Entanglement
between two spatially separated atomic modes), especially if
we can use quantum interference to measure gravitational fields.
Experimental physicists are very ingenious and I would never bet
against them. :)
Ever since writing a paper with Paul Smith
(Univ. of Washington) on Non-commutative complex differential
geometry (Journal
of Geometry and Physics 72, 2013) I have been hoping for
progress to be made on a noncommutative version of Serre's GAGA,
géométrie algébrique et géométrie analytique. Classically this is
the fact that complex manifolds (insert conditions) are the same as
complex algebraic varieties (insert conditions), and it leads to a
greater understanding of these objects than if we only had one way
of looking at them. It would be of great interest to have a
noncommutative version of GAGA. I am very glad to see that progress
is being made in this direction, with just a couple of the relevant
papers being Positive
Line Bundles Over the Irreducible Quantum Flag Manifolds by
Fredy Díaz García, Andrey Krutov, Réamonn Ó Buachalla, Petr Somberg,
Karen R. Strung and A
Kodaira Vanishing Theorem for Noncommutative Kahler Structures
by Réamonn Ó Buachalla, Jan Stovicek, Adam-Christiaan van Roosmalen.
With Tomasz Brzezinski (Swansea) I wrote The Serre
spectral sequence of a noncommutative fibration for de Rham
cohomology, Acta Mathematica 2005. This set down the
definition of a differential sheaf in noncommutative geometry,
and it has properties in line with classical sheaves including (as
the title suggests) the Serre spectral sequence. However, there are
big things missing, and to explain this I return to classical
geometry. John Milnor showed that there are several different
differential structures on the topological sphere S^7, but all of
these must have the same de Rham cohomology, because that is just
the usual topological cohomology of S^7. Now we look at quantum SU2
and at its two fundamentally different differential structures, the
3D left covariant and 4D bicovariant calculus. These have different
de Rham cohomologies, although the C* completion of both lots of
differentiable functions is the same, Woronowicz's C* algebra
quantum SU2. In fact, in noncommutative geometry there is no C*
algebra definition of a sheaf, there is just the differential
definition. However, morally the use of differentiation in the
definition of a noncommutative sheaf is absolutely minimal, it
simply is used to say that a section is `locally trivial' if it has
zero derivative. There really ought to be an alternative
definition of `locally trivial' not using a differential calculus,
but what could it be? One idea is that the theory of Quantales by
Mulvey etc. may provide a possibility...
On C* algebras, David
Evans (Cardiff) and I wrote The
real rank of algebras of matrix valued functions (Internat. J.
Math 2 (2)). This used the real rank of Brown and Pedersen, which
was based on Rieffel's topological stable rank. With Pavle Goldstein
(Zagreb) I wrote Maximal
abelian subalgebras of On (C.R. math de l'Acad. sci, Canada 21
(1)) on subalgebras of the Cuntz algebra. The paper The
braiding for representations of q-deformed affine sl2 with
Peter Johnson used complex analysis to analyse the behaviour of the
braiding for q on the unit circle in terms of the number theoretic
properties of the number τ in the deformation parameter q=e^(2πiτ).
I have been interested in topological algebras for some time,
especially as smooth function algebras (for purposes of
noncommutative differential geometry) can be expected to be
topological subalgebras of C* algebras. In Bruce Blackadar's book on
K-theory he uses the more general local C* algebras rather than C*
algebras to define K-theory. In this spirit, following the
definition of E-theory by Connes and Higson I wrote Strongly
asymptotic morphisms on separable metrisable algebras, Jour.
Funct. Anal. 177 (1), which generalises Connes & Higson's
asymptotic morphisms to a wider class of algebras.
I am also interested in nonassociative phenomena, e.g. Making
nontrivially associated modular categories from finite groups,
IJMMS 2004, ID 238947, jointly with Mohammed Al-shomrani (King
Abdulaziz University). With Ghaliah Alhamzi (Al-Imam Muhammad Ibn
Saud University and Swansea) I have written Matrices, Bratteli
Diagrams and Hopf-Galois Extensions (arXiv:2009.01577 )
<<
We show that the matrix embeddings in Bratteli diagrams are iterated
direct sums of Hopf-Galois extensions (quantum principle bundles)
for certain abelian groups>> and we are currently working and
on an exponential map for Hopf algebras generalising that for Lie
groups.
Integrable systems
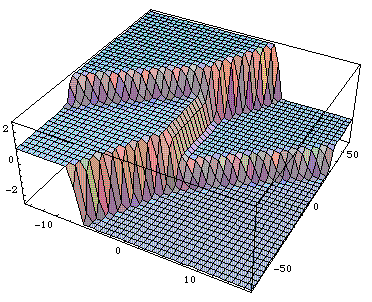
Solitons in the Principal Chiral equation. The space axis is on the
bottom left, and the time axis on the right. The function is
integrated energy density, the Morse function for the spatial
evolution. The incoming soliton on the bottom decays into two, and
one of these (the stationary soliton in the middle) in turn merges
with another soliton. This could be interpreted as a `Feynman
diagram like' interaction between two solitons mediated by another
soliton.
I completed a D.Phil. under the supervision
of Graeme Segal at St Catherine's college Oxford on the topic of
integrable systems and the principal chiral model in particular,
showing that the space and time evolution was given by Morse
functions, Solitons
in the chiral equation (Comm Math Phys. 1990). Falleh
Al-Solamy (King Abdulaziz University) and I used the energy and
momentum Morse functions given to illustrate several types of
nontrivial soliton interactions in the principal chiral model (see
the picture above).
In Swansea I worked with Peter Johnson,
�finding the inverse scattering method for solitons in a�ffine Toda
fi�eld theory in Inverse
scattering and solitons in An−1 affine Toda field theories
(Nuclear Physics B 1997) and same
title part II (Nuclear Physics B 1998), and a group
factorisation formula for the symplectic form in Loop
groups and the symplectic form for solitons in integrable theories.
In An
electrically charged monopole in quantum electrodynamics I
took advantage of the properties of the� matrices in the 4+2
dimensional Dirac equation to give a construction of a topological
electric monpole in a (higher dimensional) Kaluza-Klein type
extension of standard space time.
After finishing the book (I still prefer
not to think about how much checking went into that) I have plans to
get back to integrable systems. I would like to cooperate with
others on integrable problems, especially using geometric or
noncommutative methods. However, I have two specific projects which
I would like to do, if indeed they can be done, which is not at all
certain.
Recall that for several soliton equations
(including affine Toda, sine Gordon, principal chiral) using the
inverse scattering transform the classical phase space of the pure
soliton solutions can be visualised as a loop group consisting of
meromorphic functions. This contains all the information about the
solitons, including momenta, positions and phases. The more general
setting of the classical inverse scattering method is as a group
factorisation, or doublecross product, the problem is to find such
factorisations with Lorentzian symmetry (this itself generalises
into a theory of Hopf algebra factorisations as set down by Shahn
Majid). The quantum inverse scattering transform gives exact
matrices for the quantum scattering of solitons. There have been
examples of solitons in higher dimensions with Lorentzian symmetry
for some time, e.g. R.S. Ward, Nontrivial scattering of localized
solitons in a (2+1)-dimensional integrable system. Phys. Lett. A
208: 203-208 (1995). Recently there has been further examples and
numerical evidence of higher dimensional solitons, e.g. Y. Zarmi,
Static solitons, Lorentz invariance, and a new perspective on the
integrability of the sine Gordon equation in (1 + 2) dimensions,
Jour. Math. Phys. 54, 013512 (2013).
The questions I would like to consider are
primarily pure mathematical but with obvious applications to
integrable systems.
1) Quantum meromorphic groups: Is there a Hopf
algebra type object which has the same relation to quantum affine
SU2 as the meromorphic loop group to the analytic SU2 loop group?
(Care needs to be taken with the classical limits here.) There is a
grassmannian construction of the meromorphic loop group in terms of
representations of the analytic loop group, so that may be a place
to start. Another place to start is with the inversion of algebra
elements (much about this in An Introduction to Noncommutative
Noetherian Rings, Goodearl & Warfield, L.M.S. student
texts 16) and then see what this does to the differential geometry.
Maybe it is easiest to generalise the problem to loop Hopf algebras
using something similar to the braided constructive procedure used
by Shahn Majid for Uq(g).
2) Higher dimensional residues and group factorisations: One
way to try to find more higher dimensional integrable systems is to
use a higher dimensional variety instead of the complex numbers.
Meromorphic functions in higher dimensions have singularities along
divisors, not just points, and the geometry of the divisors can be
rather complicated. An alternative would be to look at higher
codimension singularities – to describe this let us stick to a 2D
complex manifold. A meromorphic function is one which can be locally
written as a ratio of analytic functions which are not both zero
simultaneously. Thus for (z, w) ∈ C^2 the function z/w is
meromorphic except at the point (0,0). One well known construction
is to de-singularise this by blowing up the point – replacing (0, 0)
with a copy of CP^1 , based on approaching the singular point on
various lines. However, for our purposes we really would like a
point singularity, and we recall a construction of the residue of
higher codimension singularities going back to Poincare. Following
the low dimensional case, we might attempt to implement a group
factorisation with a simple transformation of a matrix valued
codimension 2 residue at a point encoding a 2+1 dimensional
momentum. Uniqueness of the factorisation would be imposed by adding
symmetry conditions to the (mostly) meromorphic functions, and these
symmetries should be preserved by Lorentz transformation (up to a
gauge equivalence at least).
A highly speculative approach to something which
might be related to integrable systems could be the following (could
I insert any more conditionals into this sentence?). Chamseddine and
Connes have published papers related to the standard model of
particle physics and noncommutative geometry, e.g. The
Spectral Action Principle, CMP 186 (1997) (this particular
paper looks at a coupling to gravity). There has been much
discussion about whether this noncommutative model really gives the
standard model or not, and before the reader inserts an answer here
I would like to say that I am not very interested in this question.
To me the curious thing is that such a model would give anything
remotely in the right ball park, and that this is either a wild
coincidence or something rather significant. Assuming, for the sake
of argument, that it is significant, it makes sense to ask if the
noncommutative model is in itself an interesting point of view for
the study of a classical system. After all, it is a geometric
picture (noncommutative, but still geometric), and geometric
pictures have been significant in the study of physical systems
before. And why not begin with the `classical' theory of such a
system, after all that might be easier than the quantum theory. When
we are at it, we may as well simplify the system just by cutting the
sizes and dimensions down, as we are not solely interested in the
standard model. Where does that leave us? I am not at all sure, but
it sounds like an interesting adventure...
Computation and Physical systems

The Temple of Apollo at Delphi, the site of the Oracle of
Delphi
With John
Tucker (Swansea) and Felix Costa
(Lisbon) I wrote papers on the computational power and complexity of
algorithms which had access to physical information. Some of these
were also joint with Bruno
Loff (Porto),
Diogo Poças
(Lisbon), Tânia Ambaram and Pedro Cortez. See Computational
complexity with experiments as oracles (Proc. Royal Society A
2008) and Experimental
computation of real numbers by Newtonian machines (Proc. Royal
Society A 2007), Computations
with oracles that measure vanishing quantities (
Math. Struct. in Comp. Sci. 2016), Classifying
the computational power of stochastic physical oracles (Int.
J. Unconvet. Comp. 2017).
John Tucker (PI) and I were awarded the EPSRC grant EP/C525361/1
‘Foundations of computing with continuous data: algorithms versus
experiments with physical systems’, value 258,042 pounds, beginning
January 2006 and ending June 2009.
The key idea is a physical oracle, a development of the
oracle used by Alan Turing to indicate a mythical (beyond standard
computation) source of information for an algorithm. Physical
oracles to the algorithm are axiomatised abstractions, but in the
real world they can control and record data from physical
experiments. They may be error prone, and they may have a delay in
replying to queries (or never reply at all). Interestingly for
current developments, a quantum computer can be considered as a
physical oracle to a conventional algorithm.
As far as complexity theory is concerned, the key
is how much information the physical oracle can extract from a
physical system in a given time. Many experiments can be analysed,
such as Brewster's angle for measuring refractive index. The result
of reasonable assumptions on such experiments is that the time taken
to estimate a quantity to a given error is of order the error to a
negative power.
Given an independent coin toss oracle (in theory radioactive decay
can provide this), such a physical oracle has the non-uniform
probabilistic complexity class BPP//log*. Now, given the
hypothetical Planck limits on measurement, this might sound
impractical. However, the completely different independent
probabilistic oracle (e.g. a fixed finite but repeatable error)
gives precisely the same class, and this entirely independent
derivation indicates that there may be something fundamental about
BPP//log*.

`No plan survives contact with the enemy'. Helmuth von Moltke
the Elder (1800-1891)
Several piles of wreckage of space probes on the surface of Mars
testify just how difficult it is to have automated control systems
for highly complex systems in uncertain environments. Fortunately,
the accident reports for space probes and aircraft contain a wealth
of data on just how things went wrong. However, correcting one error
is not really the solution, it is necessary to build in much more
transparency and resilience into control systems. John Tucker and I
are currently working on a form of object orientated programming for
physical or even social systems. The idea is to divide the system
into modes and form a geometric model of the modes, which is
naturally a simplicial complex. The control is assigned to a mode by
using a computable partition of unity. The algorithm for a given
mode is written using a generalised many-sorted algebra. By
generalised, we mean that it contains not only sets, functions and
relations, but also physical oracles (see above). These oracles are
used to both measure and control the real world system.
Biology: Games and population
dynamics
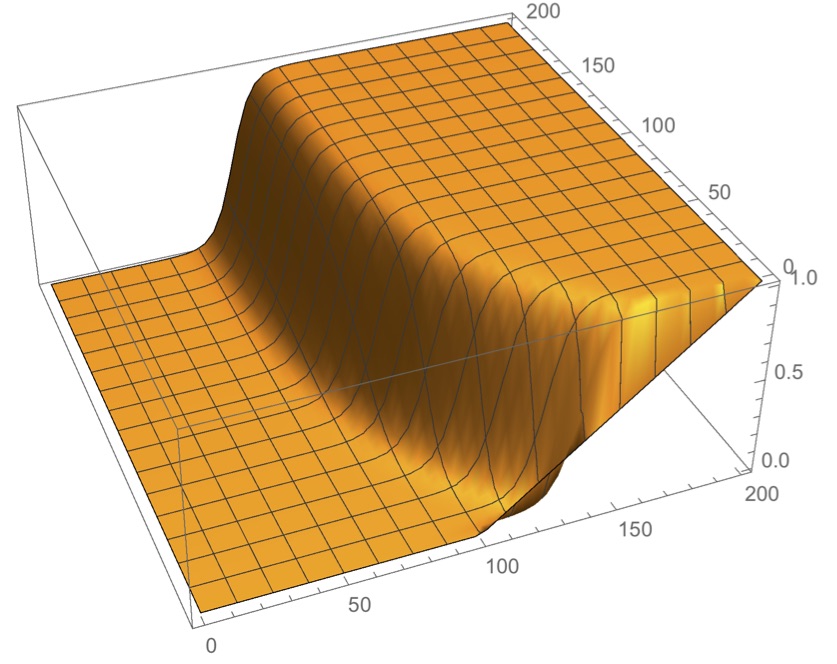
In ecology competition between different phenotypes is often
expressed in terms of a game, but its payoff coefficients may vary.
Consider an island where the direction of the prevailing wind makes
one half of the island drier than the other. A bird species has two
phenotypes, both of which would be, in isolation, stable equilibria
in both dry and wet conditions in the island. However, when
considered together, one phenotype does better in dry conditions
than the other (i.e. the other phenotype has a semistable
equilibrium). In wet conditions things are the other way around, so
the other phenotype does better. We start with wet preferring birds
on the wet side, and dry preferring birds on the dry side. Now, what
happens to the populations in the long term? The answer is that, as
long as the island is not too small, we have a stable front dividing
the phenotypes which will persist indefinitely. The exact position
of the front may shift because of slight variations in weather from
year to year, but the basic form will be unchanged. The width of the
front will be determined by the diffusion rate of the phenotypes,
basically independently of how slowly conditions change across the
island (this is why the island should not be too small). Move the
front (as in this picture, with space axis bottom right and time
axis upper right), and it springs back to its equilibrium position.
However, if the conditions vary with time, we may get a catastrophic
change at some point...
I am interested in biology in general, and am keen to find problems
in biology where mathematics can help, and people who want to
collaborate in biology.

The Great Auk Memorial, Papa Westray, Orkney
Every extinct species should have a memorial, it might remind
mankind to be more careful in future.
The tragic story of Avery, the
West Point cat.
Their buttons had all been polished
and their uniforms had been freshly pressed,
Avery's team could out-mouse the navy anytime.
Such a cat unflappable had never been seen
since Min the Mog played opposite James Dean.
Cadet Avery, the West Point cat.
One night by the Hudson the alarm went out,
there's vermin in the commander's house!
Avery mobilized his platoon without delay.
They routed the rats and massacred the mice
and victory complete was wrought in a trice.
Lieutenant Avery, the West Point cat.
The flags flew and the bugles bugled
when the president came to see around.
Avery's platoon is on guard in the kitchen
for some bandit's been stealing the presidential milk
and eating the meat and shredding the silk.
Colonel Avery, the West Point cat.
Past midnight the door creaked wider
and the squad pounced on the intruder.
Avery escorted the prisoner to the court martial.
Said general to Avery `you have mistaken the thief,
for that is the cat of the commander in chief'.
Dishonorably discharged Avery, the West Point cat.

Avery is currently in retirement at an undisclosed location in New
England.
Graphs by Mathematica.








