pgamma(4,3,1)[1] 0.7618967Lab 9 - with solutions
Please note that there is a file on Canvas called Getting started with R which may be of some use. This provides details of setting up R and Rstudio on your own computer as well as providing an overview of inputting and importing various data files into R. This should mainly serve as a reminder.
Recall that we can clear the environment using rm(list=ls()) It is advisable to do this before attempting new questions if confusion may arise with variable names etc.
Exercise 1
Let \(X\sim Gamma(3,1)\). Find \(P(X\leq 4)\) and \(P(X>2)\).
Further, let \(Y\sim Gamma(2,0.5)\). Find \(P(Y<1)\) and the value of the pdf at \(y=3\). Create a plot of \(Y\sim Gamma(2,0.5)\).
Hint: Adapt the R code met previously for other distributions. In particular, the help("pgamma") R code should be useful in determining the arguments/options.
Solution
help("pgamma")- \(P(X\leq 4):\)
- \(P(X>2):\)
1-pgamma(2,3,1)[1] 0.6766764Or
pgamma(2,3,1,lower.tail=F)[1] 0.6766764\(P(Y<1):\)
pgamma(1,2,0.5)[1] 0.09020401and the value of the pdf at y=3:
dgamma(3,2,0.5)[1] 0.1673476- The plot of \(Y\sim Gamma(2,0.5)\).
We first create a sequence of numbers (inputs) between 0 and 20 and then find the corresponding values of the distribution function. Finally we plot these against each other.
y<-seq(0,20, length=10000)
dy<-dgamma(y,2,0.5)
plot(y,dy, xlab="y value",type="l", ylab="Density", main="Gamma(2,0.5) Distribution")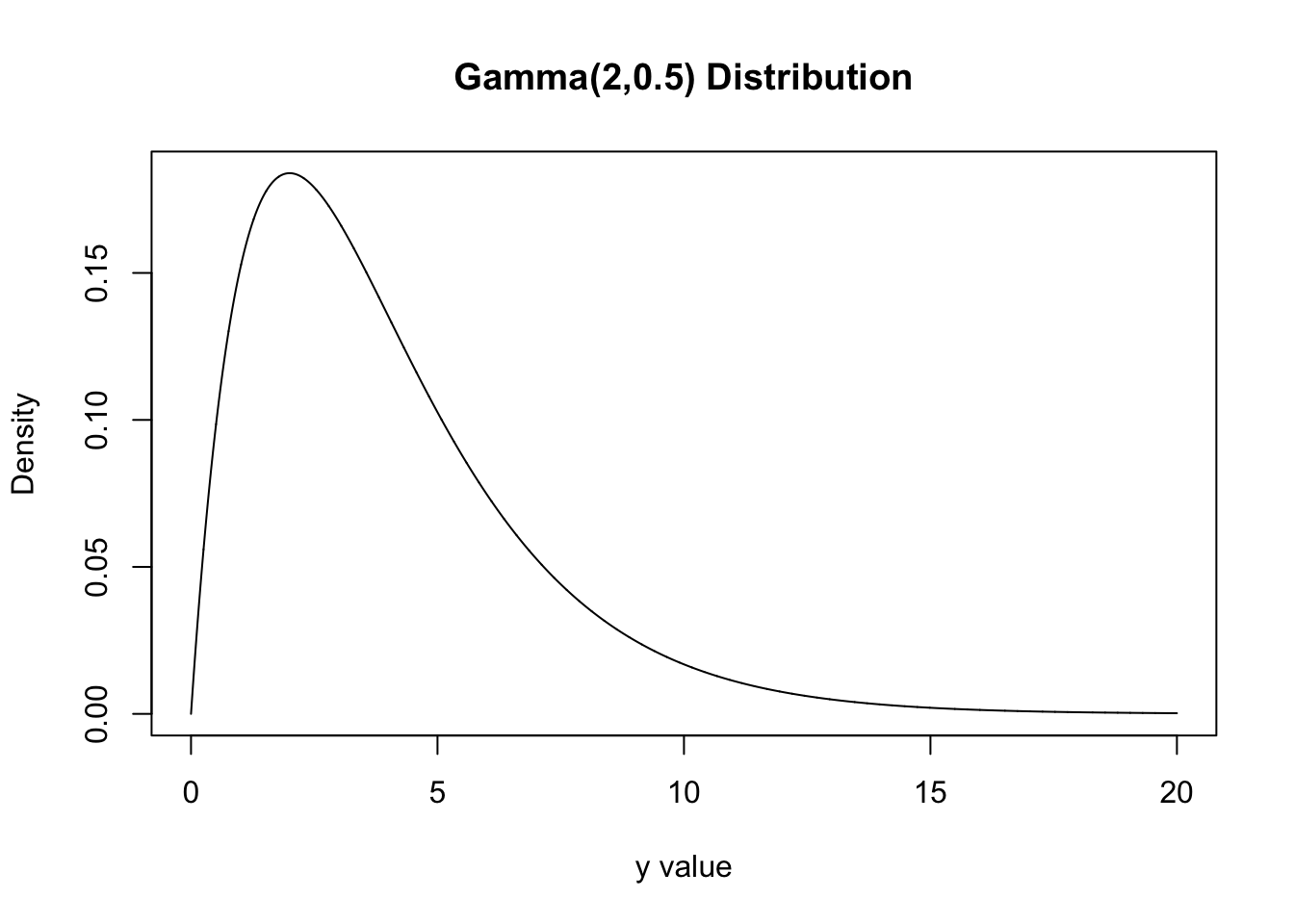
Example 1
In this example we will perform a gamma regression on an in-built dataset in R (wafer) using the log link function. The outcome is measuring resistance of a wafer in a physics experiment. The predictor/independent variables are \(x_1,\ldots,x_3\).
- We first install the dataset and visualise it:
install.packages("faraway")library(faraway)
data(wafer)
plot(density(wafer$resist))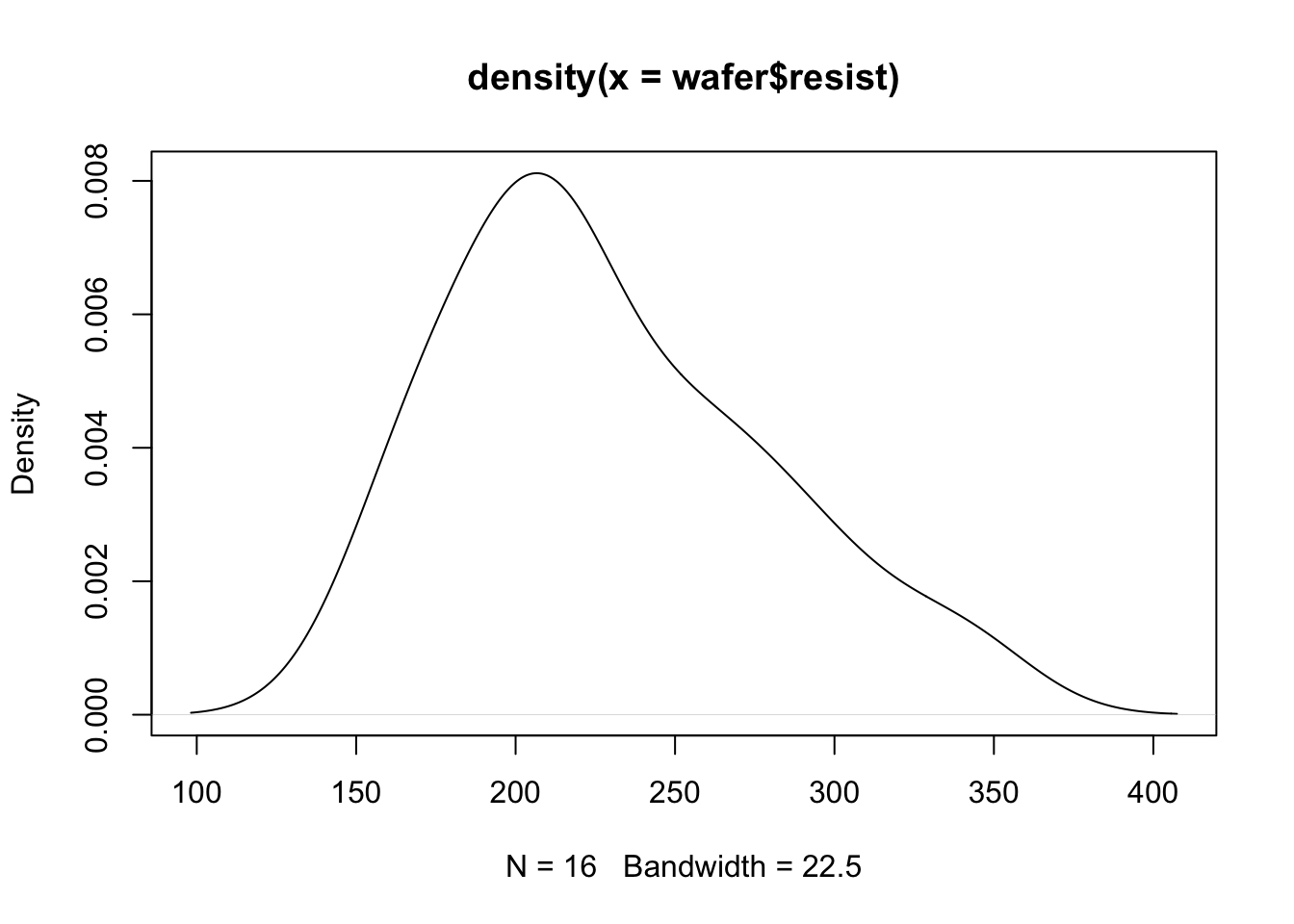
- The plot looks skewed, therefore we will check whether it follows a gamma distribution using a Kolmogorov-Smirnov test. Using the help function we see that we will need to enter the parameters (shape and rate) of the distribution that we are testing against. To obtain these we use fitdistr, see below,
help("ks.test")
library(MASS)
help("fitdistr")
fitdistr(wafer$resist, "gamma") shape rate
23.09377758 0.10072802
( 8.09441180) ( 0.03568919)ks.test(wafer$resist, pgamma, shape=23.1, rate=0.1)
Exact one-sample Kolmogorov-Smirnov test
data: wafer$resist
D = 0.16066, p-value = 0.7458
alternative hypothesis: two-sided- The test is not significant, hence the data seem to follow a gamma distribution with parameters as calculated above. We now proceed to calculate the model. Note that we do not use the canonical link function, i.e. the inverse function, but instead we use the log link function.
GammaReg <- glm(formula = resist ~ x1 + x2 + x3,
family = Gamma(link = "log"),
data = wafer)
summary(GammaReg)
Call:
glm(formula = resist ~ x1 + x2 + x3, family = Gamma(link = "log"),
data = wafer)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.41553 0.05305 102.083 < 2e-16 ***
x1+ 0.12110 0.05305 2.283 0.041474 *
x2+ -0.29981 0.05305 -5.651 0.000107 ***
x3+ 0.18240 0.05305 3.438 0.004909 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Gamma family taken to be 0.01125723)
Null deviance: 0.69784 on 15 degrees of freedom
Residual deviance: 0.13741 on 12 degrees of freedom
AIC: 152.53
Number of Fisher Scoring iterations: 4The output above shows the significance of the predictor variables and the coefficients
Finally, we evaluate the model using Deviance
anova(GammaReg, test="Chisq")Analysis of Deviance Table
Model: Gamma, link: log
Response: resist
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 15 0.69784
x1 1 0.05059 14 0.64725 0.0340206 *
x2 1 0.37740 13 0.26985 7.034e-09 ***
x3 1 0.13244 12 0.13741 0.0006035 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Please note the significance of the model from the output above.