Lab 4 - with solutions

Please note that there is a file on Canvas called Getting started with R which may be of some use. This provides details of setting up R and Rstudio on your own computer as well as providing an overview of inputting and importing various data files into R. This should mainly serve as a reminder.

Recall that we can clear the environment using rm(list=ls()) It is advisable to do this before attempting new questions if confusion may arise with variable names etc.

Example 1

In this example we will calculate various probabilities and critical values of chi-square distributions.

  • Firstly, we let \(X\sim\chi_4^2\) and we calculate \(P(X\leq1.5)\). Use the following code to calculate this (the help function might help you adapt the code):
help("pchisq")
pchisq(1.5,4)
[1] 0.1733585
  • Next use the following code to calculate \(P(X\geq0.25)\)
pchisq(0.25,4, lower.tail=F)
[1] 0.992809
  • We now turn to critical values and calculate \(\chi_{0.05,9}^2\)
qchisq(0.05,9, lower.tail = F)
[1] 16.91898
  • Finally, we calculate \(\chi_{0.01,12}^2\)
qchisq(0.01,12, lower.tail = F)
[1] 26.21697

Exercise 1

a Let \(Y\sim\chi_7^2\), calculate \(P(0.5\leq Y<5.2)\). b Calculate the critical values \(\chi_{0.05,5}^2\) and \(\chi_{0.005,5}^2\).

Solutions

  • \(P(0.5\leq Y<5.2)\):
pchisq(5.2,7)-pchisq(0.5,7)
[1] 0.3638756
  • Critical values for Chi-square, 5 df, \(\alpha=0.05\) and \(\alpha=0.005\):
qchisq(0.05,5, lower.tail = F)
[1] 11.0705
qchisq(0.005,5, lower.tail = F)
[1] 16.7496

Example 2

In this example, we will perform the exam classification example, Example 3.1 in the lecture notes, in R. Recall that in this example we want to perform a chi-square goodness-of-fit test on the exams classification dataset below:

A B C D E
Observed (\(y_i\)) 32 48 71 30 19
Expected (\(\tilde{y}_i\)) 20 40 80 40 20

  • Note: clearly the categories are independent and the expected frequencies are all \(\geq5\), hence satisfying the assumptions for categorical variables.

  • We first input the variables as below:

Class<-c("A", "B", "C", "D", "E")
Observed<-c(32,48,71,30,19)
Expected<-c(20,40,80,40,20)
  • We require expected proportions and not expected frequencies to perform the chi-square goodness-of-fit test in R, hence we create a new “prop” variable. The code below also creates a dataset from the inputted variables.
prop<-Expected/200
prop
[1] 0.1 0.2 0.4 0.2 0.1
ExamClass<-data.frame(Class,Observed,Expected,prop)
  • Now we perform the chi-square goodness-of-fit test.
chisq.test(Observed,p=prop)

    Chi-squared test for given probabilities

data:  Observed
X-squared = 12.363, df = 4, p-value = 0.01485

  • You should obtain a p-value of \(0.01485<0.05\) as per the above output, therefore we reject the null hypothesis that the exam results follow the expected distribution. Note that this does not highlight where the discrepancies lie.

  • We next produce side-by-side bar charts to visualise the observed versus expected frequencies. We must first create a matrix containing the observed and expected frequencies, see below.

ExamClassMatrix<-matrix(c(32,20,48,40,71,80,30,40,19,20), nrow=2,
              dimnames = list(c("Observed","Expected"), c("A","B","C","D","E")))
ExamClassMatrix
          A  B  C  D  E
Observed 32 48 71 30 19
Expected 20 40 80 40 20
barplot(ExamClassMatrix,
        beside=TRUE,
        ylim=c(0, 100),legend=T, col=c("yellow","blue"),
        xlab="Exam Classifications",
        ylab="Frequency")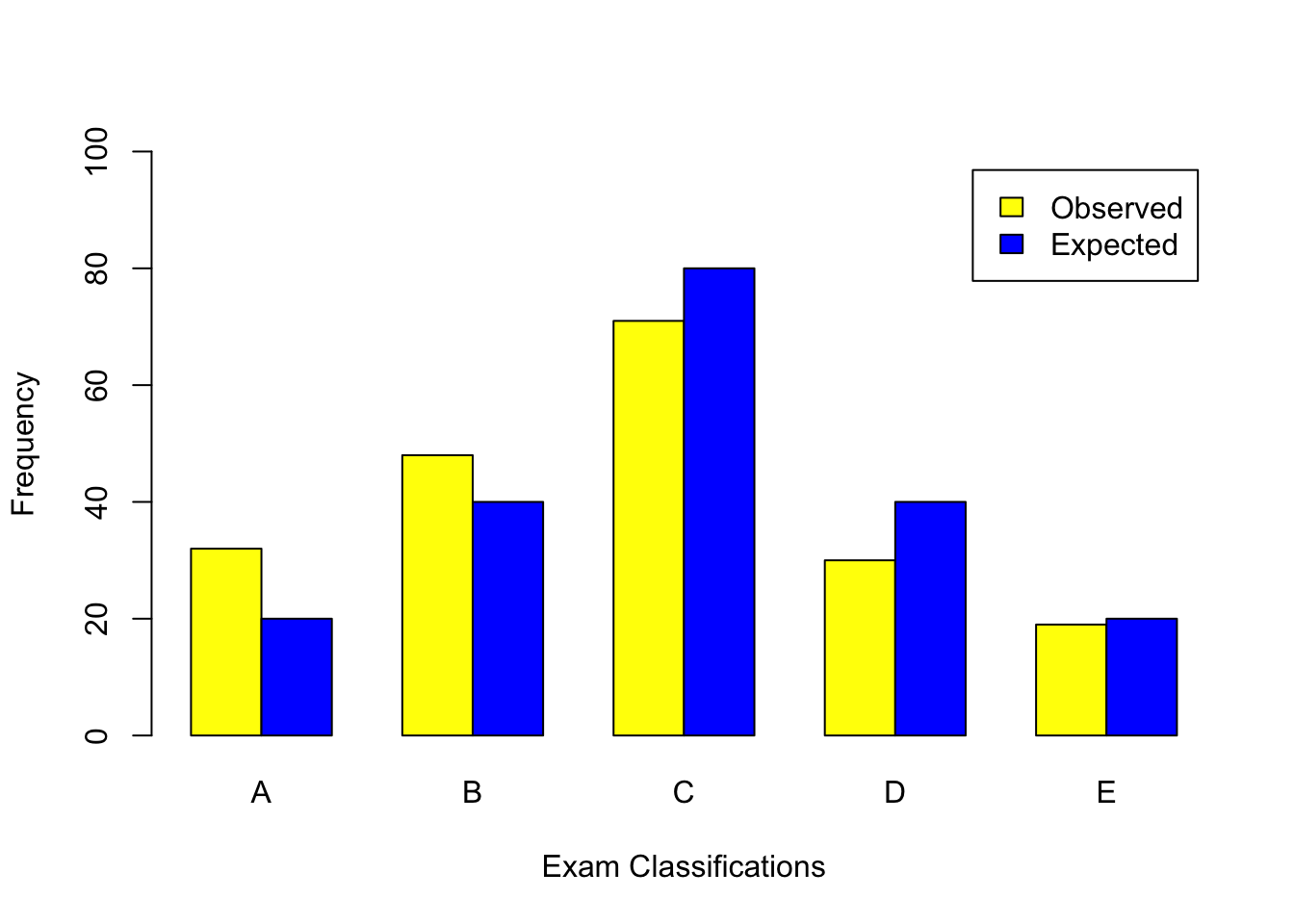

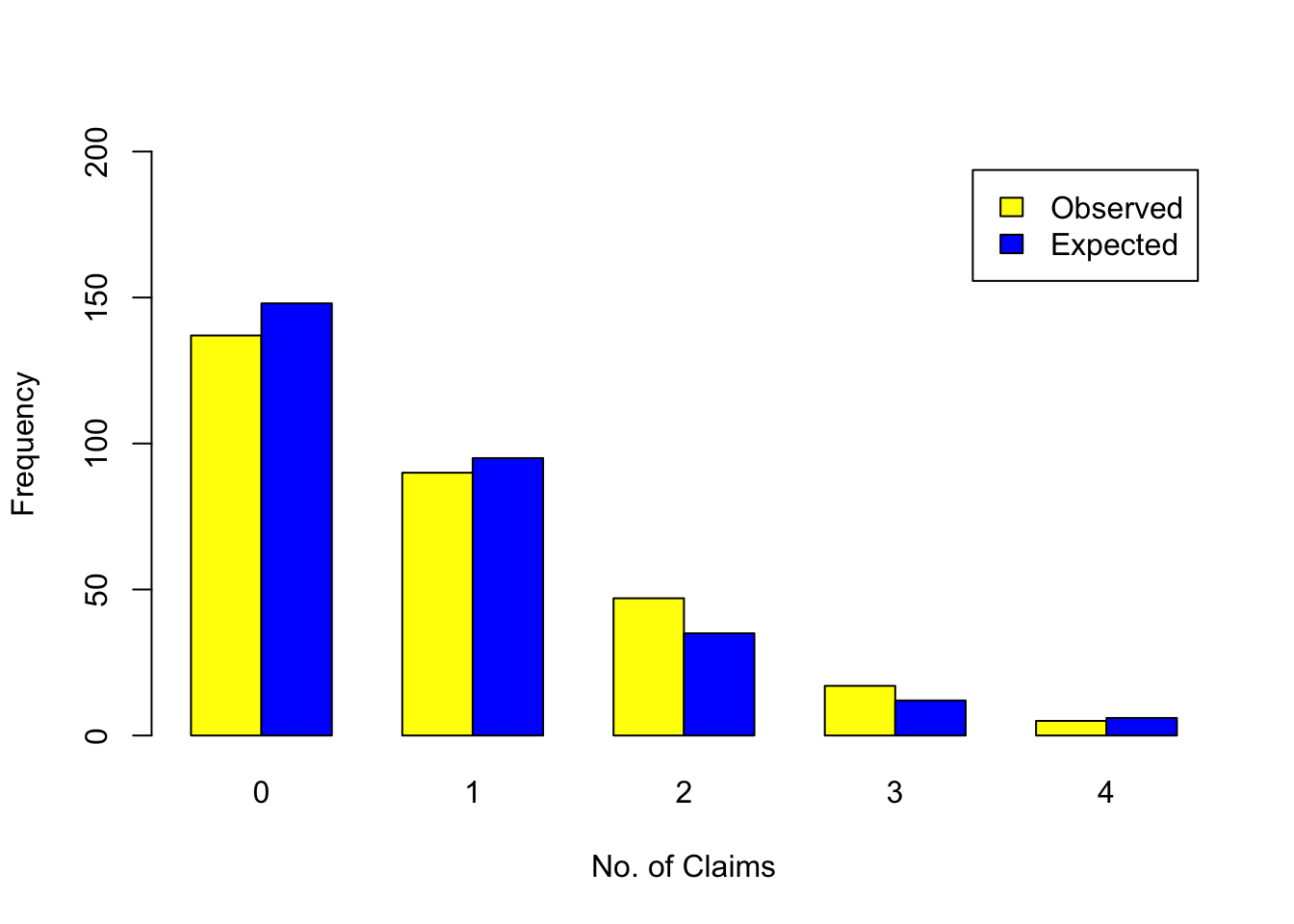
  • This output echos the results obtained above.

Exercise 2

The table below contains the observed and expected number of car insurance claims per policy holder in a given year.

Claims: 0 1 2 3 4
Observed 137 90 47 17 5
Expected 148 95 35 12 6

Checking the assumptions for categorical variables, perform a \(\chi^2\) goodness-of-fit test on this dataset.

Solution

  • We first enter the data
Claims<-c(0,1,2,3,4)
Observed2<-c(137,90,47,17,5)
Expected2<-c(148,95,35,12,6)
  • We require expected proportions and not expected frequencies in the R chi-square test, hence we create a new “prop” variable
prop2<-Expected2/296
  • Here we create the dataset.
ClaimsData<-data.frame(Claims,Observed2,Expected2, prop2)
ClaimsData
  Claims Observed2 Expected2      prop2
1      0       137       148 0.50000000
2      1        90        95 0.32094595
3      2        47        35 0.11824324
4      3        17        12 0.04054054
5      4         5         6 0.02027027
  • Next we perform the chi-square goodness-of-fit test
chisq.test(Observed2,p=prop2)

    Chi-squared test for given probabilities

data:  Observed2
X-squared = 7.445, df = 4, p-value = 0.1142

  • The p-value is 0.1142 therefore we do not reject the null hypothesis and conclude that the data is as expected.

  • Finally, we produce bar charts of the observed and expected frequencies for each claims number.

ClaimsMatrix<-matrix(c(137,148,90,95,47,35,17,12,5,6), nrow=2, dimnames = list(c("Observed","Expected"), c("0","1","2","3","4")))
ClaimsMatrix
           0  1  2  3 4
Observed 137 90 47 17 5
Expected 148 95 35 12 6
barplot(ClaimsMatrix,
        beside=TRUE,
        ylim=c(0, 200),legend=T, col=c("yellow","blue"),
        xlab="No. of Claims",
        ylab="Frequency")

Back to top